By Deanna Kerry, New Science Communicator Guest Blogger
Physics is the foundation of all sciences. It provides fundamental laws that describe how objects move and interact with one another. Any system can be examined from the perspective of physics, even things that would normally be thought of as biology or chemistry.
To understand difficult concepts, physicists often build models. This means that they strip away the details of a system and look at its most fundamental properties. This approach can also be applied to cells, which are extremely complex structures with many interconnected mechanisms. Understanding the physics behind these mechanisms, especially cell division, is very challenging.
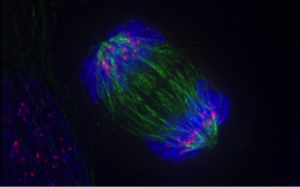
Cell division is a process with many steps. I am a biophysics researcher and my lab is especially interested in anaphase. This is when chromosomes move to opposite parts of the cell, drawn away from one another by spindle fibres towards the poles of the cell.
A cell during anaphase. (Roy van Heesbeen of Delta Vision Roy van Heesbeen, Public Domain)
This process occurs in eukaryotes, which are organisms whose cells contain a nucleus and other organelles enclosed within membranes. These include plant, animal, and fungus cells. Anaphase in eukaryotes is well understood among biologists. Anaphase in bacteria is another story.
Bacteria are simple structures, much less complicated than eukaryotic cells. Bacterial cells lack the structures that facilitate chromosome segregation. There are no spindle fibres, no centrioles, or anything else – nothing that aids in moving each chromosome to the corresponding daughter cell.
This simplicity raises the question: What could possibly drive the chromosomes apart after replication? Statistical physicists have an idea: entropy.
Entropy is a notoriously difficult concept to explain, even in classes focused on statistical mechanics. It can be described as a measure of the dispersal of energy. High entropy means that the energy of a system is very spread out among its components.
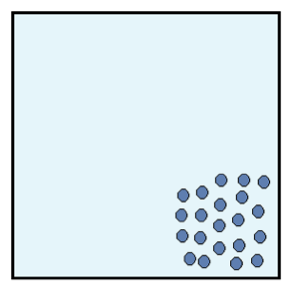
Figure 1: Initial system configuration.
According to the second law of thermodynamics, the entropy of an isolated system – that is not gaining or losing energy – will always increase.
Picture an isolated box filled with identical particles that can move around but must remain inside the box. The particles start out in a configuration like the one in the image below. They are very close together and do not take up the entire volume of the box.
Each identical particle carries the same amount of energy. Because the particles are so close together, the energy is not dispersed throughout the system. We say that the entropy of this system is low. The second law of thermodynamics tells us that after some time, the box of particles will look like Figure 2.
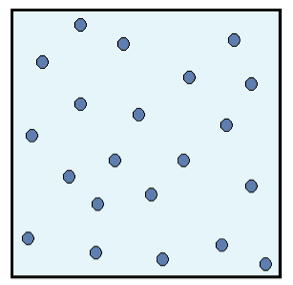
Figure 2: Final configuration of the system.
The particles are spread out evenly, which means that the energy is also dispersed evenly inside the system. Because of this dispersal of energy, we say that the entropy of the system is high.
These concepts can be applied to chromosomes, too. Chromosomes that exist in a neat, ordered state inside a cell will inevitably become disordered as time progresses and the system’s energy is dispersed. To understand how entropy plays a part in chromosome segregation, we first need a model of chromosomes inside the cell. Then we can examine what happens to the orientation of the chromosomes as the system is left to evolve.
It is not feasible to model every detail of a chromosome, but even when we greatly simplify it we can still gain information relevant to the physics of the cell. We can model the chromosomes as simple, hard spheres connected in a ring – like a string of pearls. This is a polymer: a series of connected identical molecules called monomers. Polymer physics is a wide and varied field that has applications outside of biophysics, but the study of chromosomes is a major focus of research for polymer physicists.
Figure 3: My polymer simulation
The polymers in our model are given certain movement rules to follow. For example, the monomers must not get too close to each other and merge, because they cannot do this in real life. And the polymer must always remain in a ring shape. Once we have a model that accurately reflects how polymers behave, we can perform simulations under different conditions. The simplicity of the model makes it possible to run efficient simulations for large polymers that quickly yield results, allowing us to gather a lot of quantitative information about the polymer’s behaviour.
To represent chromosomes in a bacterium, we usually put two of these polymers in a simulated cylinder. These polymers move around randomly and tend to get in each other’s way if they are close together.
If two polymers are placed so they overlap each other, they will move away from one another towards opposite sides of the cylinder.
Figure 4: Polymers segregating.
We can explain this using entropy. When the polymers are overlapping, they are close together and compacted. This means the polymers’ energy is not dispersed throughout the cylinder, a state that is analogous to Figure 1. When the polymers separate from one another, they are not crowded together and can take up more space. This means that the energy is dispersed throughout the cylinder, as seen in Figure 2. The second law of thermodynamics tells us that this is the optimal state. This could explain what causes chromosomes to separate after replication in bacteria!
Chromosomes aren’t the only things inside a bacterium, however. There are other objects that might influence the physics of the segregating chromosomes. This means that we have to add objects to our model to see how they influence the system’s behaviour. In my model, I use simple, hard spheres as a stand-in for other cellular objects. The spheres don’t interact with the polymers, but they do take up space and crowd them.
Figure 5: Adding crowding agents.
The addition of crowding agents changes the energy of this system. When there are no crowding agents, the difference in entropy between overlapping and non-overlapping states is quite large. When there is a high density of crowding agents, this difference is much smaller. The biggest goal of my project right now is determining the process by which this occurs. Its relevance to chromosome segregation has not yet been determined, though it appears that the presence of crowding agents compacts the chromosomes, behaviour that has been noted in E. coli bacteria.
Our model focuses on bacterial chromosomes, but it has uses in other more general contexts in biophysics. The simulation of confined polymers is useful for exploring the behaviour of translocating proteins, protein folding, the movement of viruses, and determining possible faster and cheaper methods for sequencing DNA.
My project is also an important reminder that the laws of physics influence all areas of science in one way or another and we must take this into account when doing almost any scientific study.
