By Jeremy Lane
Math & Stats subject editor
In the oft-repeated story of the development of the theory of motion, it was Aristotle who postulated (between 335 and 323 BC) that heavier objects fall faster, while Galileo triumphantly refuted him in the early 17th century by proving that the distance travelled by a falling object is proportional to the square of the time elapsed, and is actually independent of the object’s weight.
This version of the story is like much of the popular history of science, which often glosses over the long history involved in the development of key scientific concepts. Ultimately, it neglects a millenium of intervening research on the nature of motion performed in the Roman empire, the Islamic world, and high-late medieval Europe – specifically in Italy, France and England.
Fruitful European* study of Aristotle’s ideas about motion began in the 13th century, when Latin translations of his and other Greek philosophers’ work (notably that of Euclid) began to appear. In the 14th century, medieval scholars made a number of crucial refinements and contributions to Aristotle’s ideas, laying the groundwork for Galileo’s later progress. Primary among these scholars were four members of Merton College at Oxford: Thomas Bradwardine, William Heytesbury, Richard Swineshead, and John Dumbleton. They have since come to be known as the Oxford Calculators.
According to the exhaustive research of Clagett [2], the Oxford Calculators had four main original contributions to the theory of motion:
- clearly distinguishing between kinematics and dynamics,
- defining instantaneous velocity,
- defining uniform acceleration, and
- describing uniformly accelerated motion.
The distinction between the properties (kinematics) and causes (~dynamics) of motion was crucial and freeing, as it allowed the Calculators to focus on kinematics directly. Prior scholars had been bogged down by the paradoxes of Aristotle’s ideas about causation. Precise definitions of the properties of motion as quantities represented by ratios of other quantities allowed the Calculators to work with the concepts numerically, a significant step beyond Aristotle’s qualitative and vague descriptions [3].
Most notably, and relying fundamentally on the first three contributions, the Oxford Calculators provided an accurate description of uniformly accelerated motion by stating the mean speed theorem – although in their context it was only a postulate with numerical evidence.
As stated later by Galileo, the mean speed theorem says that:
“The time in which any space is traversed by a body starting from rest and uniformly accelerated is equal to the time in which that same space would be traversed by the same body moving at a uniform speed whose value is the mean of the highest speed and the speed just before acceleration began.” [5]
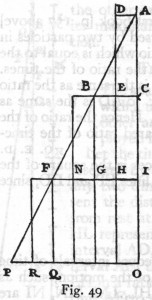
A diagram from Galileo’s Two New Sciences demonstrating the distance traversed over equal time intervals by uniformly accelerated motion.
Compare Galileo’s text with this excerpt from Heytesbury (1338):
“With respect, however, to the distance traversed in a uniformly accelerated motion commencing from zero degree [speed] and terminating at some finite degree, it has already been said that the motion as a whole, or its whole acquisition, will correspond to its middle degree…From the foregoing it can be sufficiently determined, for this kind of acceleration or deceleration, how great a distance will be traversed, all other things being equal, in the first half of the time, and how much in the second half. For when the acceleration of a motion takes place uniformly from zero degree to some degree, the distance it will traverse in the first half of the time will be exactly one third that of which it will traverse in the second half of the time.” ** [2,3]
Heytsebury’s quote demonstrates the level of mathematical technology used by the Oxford Calculators: they had access to Euclid’s geometry and some Arabic trigonometry, but not algebra. So rather than providing logical proofs, they gave numerical and geometric demonstrations, thus earning their name as calculators. Relying on concepts established by Euclid, their work described proportions of quantities and related these to other proportions and quantities (e.g., by defining average speed as v = (d_2 – d_1)/t) [2]. This approach had a precursor in the 1328 work of the Parisian philosopher John Buridan, whose application of the Euclidean notion of proportion to motion is arguably the first [2]. However, Buridan’s work was largely obsessed with Aristotle’s causes of motion and therefore did not yield the same progress as the Oxford Calculators [1,3].
Despite making these significant conceptual leaps, it is perhaps surprising that the Oxford Calculators never identified falling objects or inclined planes as examples of uniformly accelerated motion [3]***. In the spirit of Aristotle, their work remained strictly theoretical. and there is no evidence that they conducted any actual experiments [2].
The Oxford Calculators’ works were widely distributed in Latin and studied**** across Europe, and their progress survived into the Renaissance, where it influenced scientists such as Galileo [4]. If you’re interested in more about the history of motion, or want to learn how Galileo and other Renaissance scientists built on the work of medieval scholars, then I highly recommend History of Free Fall: Aristotle to Galileo by Stillman Drake, which is full of historical delights.
*Though not the focus of this post, earlier medieval work also occurred in the Islamic world; translations and commentaries by Avicenna and Averros were among those that directly influenced the western work.
**For illustration, compare this last sentence with the diagram below from Galileo’s Two New Sciences.
***The first known statement that free fall is an example of uniformly accelerated motion appears in a 1550 work of Domingo de Soto, although he provides no explanation for the claim [3]. The first experimental confirmation of this fact is due to Galileo.
****Notably by the 14th century French scholar Nicholas Oresme, who would continue their study of uniformly accelerated motion.
References:
[1] http://plato.stanford.edu/entries/buridan/
[2] Clagett. The Science of Mechanics in the Middle Ages. 1959.
[3] Drake. The History of Free Fall. 1989.
[4] Truesdell. Essays in the History of Mechanics. 1968.
[5] Galileo. Two New Sciences. 1638.




One thought on “Exploring the history of the math of motion”
Comments are closed.