Malgosia Ip, Mathematics & Statistics editor
In just over four weeks, your neighbourhood might be overrun by zombies. No, it’s not the end of the world. It’s Halloween: the one day of the year when it’s OK for your kids to wander the streets in search of a sugar high.
But you’re not just any parent – you’ve got important things to do and Netflix shows to watch. You want to make sure you hit all the streets in the neighbourhood in the shortest possible time.
So how do we figure out the optimal route? We ask a Chinese postman.
The Chinese postman problem
The Chinese postman is a mathematical problem in the field of graph theory that aims to find the shortest possible route along a set of streets. It’s pretty easy to see the parallels between this problem and our Halloween scenario. We both want to find the shortest route along all the streets in the neighbourhood, but instead of delivering mail, we’re collecting candy.
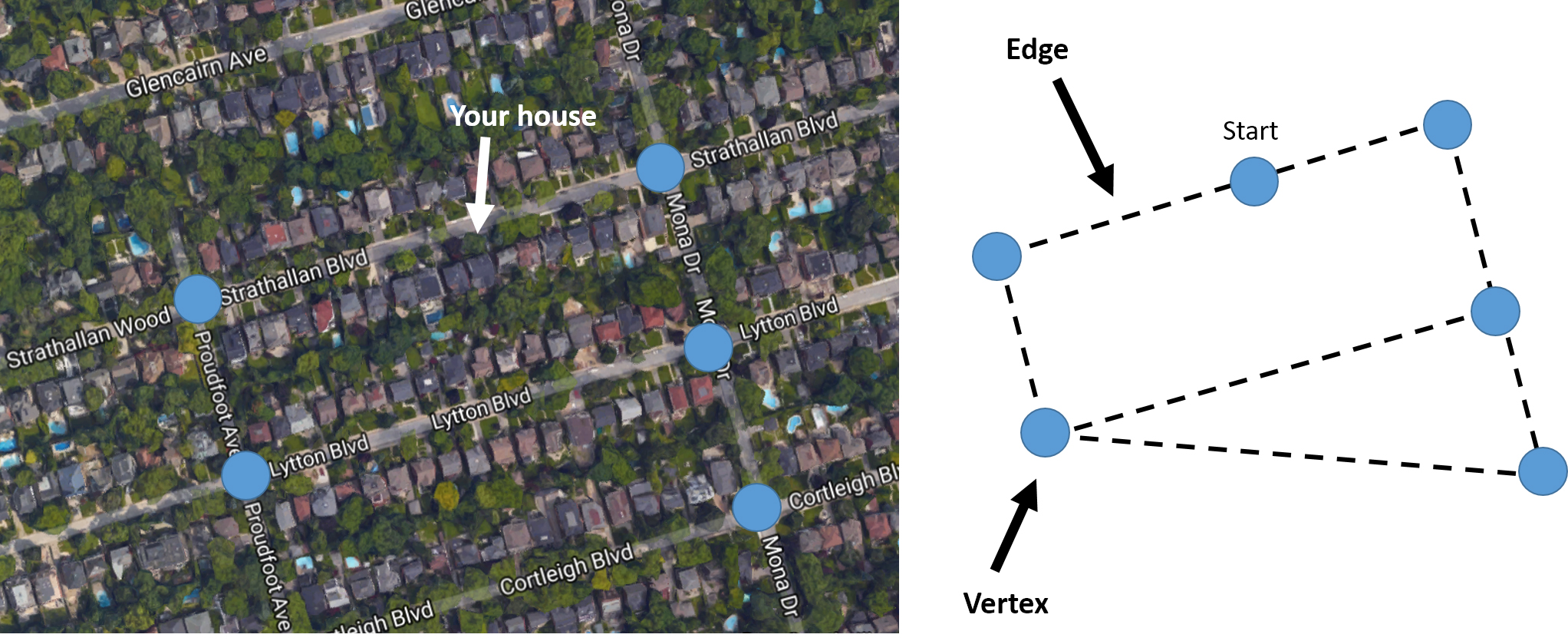
To start with, we need to look at our neighbourhood map as a graph, that is as a set of vertices (in our case, intersections) connected by edges (streets). We want to find the shortest possible route that goes along every edge at least once.
We could dive right in and try drawing a route, but to make sure we get the shortest one, we’d have to find all the possible routes and compare them. This is called the brute force approach and not only is it tedious, but it takes longer and longer to find the solution the more streets we add.
What we need is an algorithm: a set of instructions or equations we can use that can solve the problem faster than the brute force approach.
Before we go any further, though, I have to introduce some mathematical terminology. We need to determine whether or not our graph is Eulerian. If it is possible to travel along the entire graph using each edge only once, then it is Eulerian. Way back in the 1700s, Leonhard Euler proved that this is possible if, and only if, all the vertices of the graph are even – that is, they have an even number of edges connected to them.
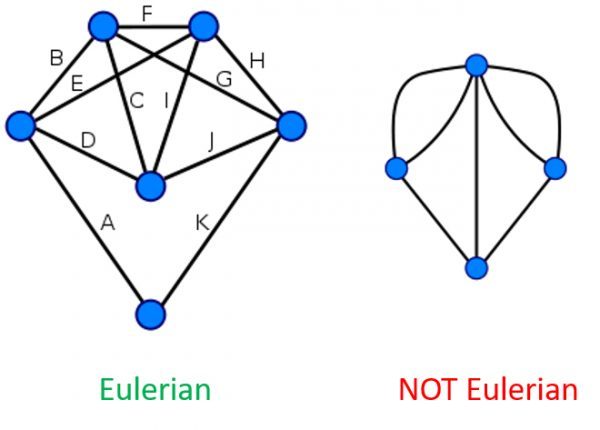
The definition of Eulerian has nothing to do with complexity. The graph on the left is Eulerian (every vertex is even) and the one on the right is not. Go ahead and check!
If our graph is Eulerian, then our job is done. The path that crosses each edge only once is by definition the shortest path, and we can find it using an algorithm like the Hierholzer method. I won’t go into the details of the Hierholzer method, but this website has a great step by step explanation of it.
If our graph is not Eulerian, then we need to make it Eulerian. Mathematicians like doing that sort of thing – it’s not about finding a brand new solution, it’s about making your problem look like something that already has a solution.
To make any graph Eulerian, we need to double up on some edges so that all the vertices become even. But there’s one more catch: because we’re trying to find the shortest route, we need to make sure the length of the edges that we’re adding is minimized. In the simple example below, we would add an edge from A to B to make all vertices even again.
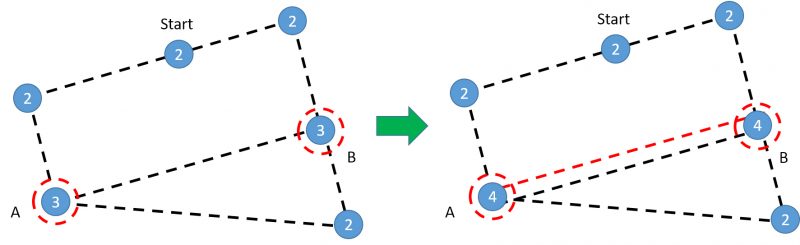
By adding one edge between the two odd vertices A and B, we can transform the graph on the left (not Eulerian) into the graph on the right (Eulerian). Numbers indicate how many edges connect to each node.
Adding edges in more complex examples, however, presents a completely new and different problem. It’s called a matching problem, because you want to match odd vertices together so that they become even.
Enter Canadian mathematician Jack Edmonds who, in the early seventies, was working at the relatively new University of Waterloo Department of Combinatorics and Optimization. Edmonds devised an algorithm to solve the matching problem in “polynomial time” – that’s math-speak for relatively quickly and is like the holy grail for all algorithms. He called his solution the Blossom algorithm because it looks for closed loops within a graph, which can resemble flowers. Edmond’s algorithm also works for any type of graph, unlike other algorithms like the Hungarian method.
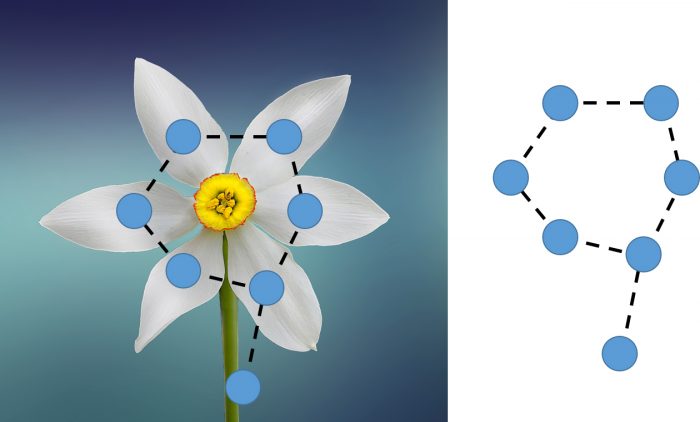
Edmond’s matching algorithm is called the Blossom algorithm because of the way it treats closed loops in graphs, which can resemble flowers.
Of course, if you want to find your optimal Halloween route using these methods, you’ll still need to create a program using the right algorithms or find some ready-made code – because there is no mathematical trick that allows you to solve the problem by hand or in your head. But thanks to Edmonds’ algorithm, any optimal trick-or-treating route can be found efficiently, no supercomputers required.
Now if only there were an algorithm for dealing with sugar-filled children.
~30~