Chenoa van den Boogaard, Physics & Astronomy editor
The world is a bustling place, naturally chaotic and unpredictable, yet a balance is found in the regularity of nature’s cycles and patterns. The rise and fall of the sun and moon, the passing of the seasons, and the arrival of each hour in the day keep us grounded as we navigate our busy lives. Repeating patterns in nature, such as the symmetrical arrangement of petals on a flower or the regular series of notches on a pine cone, help us to find logic and order in our lives.

Examples of the Fibonacci spiral in nature. Clockwise from top left: a cross-section of a seashell, a pinecone, an aloe variety, and a leaf. Image sources: Wikipedia, CC BY-SA 3.0; Flickr, CC BY-NC-SA 2.0; Wikipedia, CC BY 2.0; and Flickr, CC BY-NC-ND 2.0
While these patterns bring a sense of calm and understanding, they also spark our curiosity. Why do flower petals arrange themselves so symmetrically and a fork of lighting remind us so much of the structure of a tree? Are such things just a coincidence, a simple trick of nature? Or is there something deeper at play?
These questions have been pondered and discussed from as early as the 6th century BCE by Greek and Indian philosophers. Some of the first insights were made when philosophers noticed that flowers usually grow a certain number of petals (often 3, 5, 8 and 13) and tree trunks gain successive growth rings as they age. These early observations inspired the idea that it might be possible to represent patterns in nature numerically. Shortly after this idea began to gain momentum, observers noticed that certain numerical sequences and ratios occurred over and over again in the natural world.
Leonard Bonacci and the Golden Ratio
In the 13th century, Italian mathematician Leonardo Bonacci travelled to India on a quest to broaden his understanding of mathematics and further his study of the patterns he observed in nature. Indian mathematicians had moved away from Roman numerals, which were cumbersome and limiting. They expanded the Hindu-Arabic number system to include the concepts of negative numbers and zero, creating the numerical system we use today. Bonacci was fascinated by the new advances in mathematics that the eastern world offered and introduced them to the western world through his book Liber Abaci.
Bonacci frequently went by the name Fibonacci (short for filius Bonacci, meaning ‘son of Bonacci’), and it was this name that was given to one of the more fascinating mathematical relationships in his book.
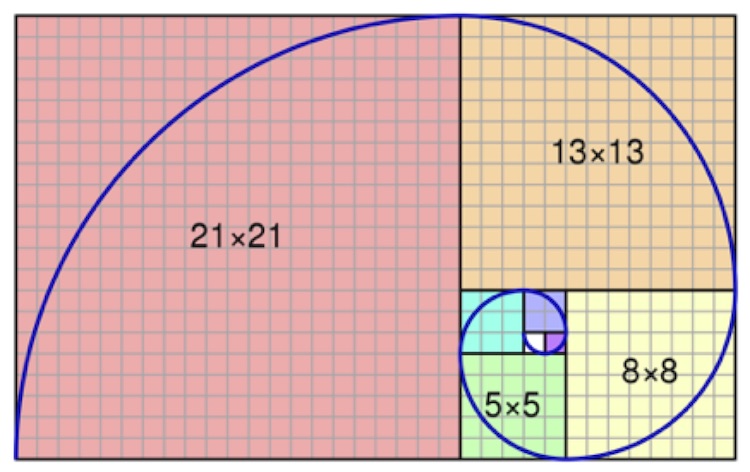
The Fibonacci spiral. The side of each large square represents a number in the Fibonacci sequence, while quarter-circle arcs connect opposite corners within each square. Image source: Wikipedia, CC0

The seeds in the head of a sunflower arrange themselves in Fibonacci spirals.
Image source: Wikipedia CC BY-SA 2.5
The Fibonacci sequence is an infinite series of numbers starting with 0 and 1 where each number in the series is the sum of the two numbers preceding it 0,1,1,2,3,5,8,13,21,34, etc. The fascinating aspect of this sequence is that it describes so many natural forms. The number of petals on a flower, branches on a tree, and seed arrangement within the head of a sunflower usually fall within the Fibonacci sequence.
The most famous and extensively studied offshoot of the Fibonacci sequence is a special mathematical relationship called the golden ratio, sometimes referred to as the ‘divine proportion’. This number is approximated by 1.618 (represented by the Greek letter phi). The golden ratio is the product of any given number in the Fibonacci sequence divided by the number that directly precedes it in the series. The further you travel along the sequence the closer you get to 1.618. The golden ratio can be seen in seashells, spiral galaxies, waves, and even in human faces.
Nature is lazy
Although the Fibonacci sequence and golden ratio are found extensively throughout the natural world, they do not represent everything in nature. Some flowers sprout a number of petals that do not fall within the Fibonacci sequence and many galaxies form in non-spiral formations. So what is governing these areas of nature?
It turns out that mathematics does form the blueprint of our natural world, but nature’s behaviour cannot be summed up by one ratio or sequence. Several mathematical relationships that explain the complex facets of nature and collectively they reveal a single basic fact: nature is lazy.
The natural world will always arrange itself in such a way as to expend the least amount of energy to gain the greatest benefit. This is why tree branches grow by spreading out while filling space efficiently, why atoms arrange themselves in specific, energetically favourable formations, and why spirals and circles, both of which are energetically favourable shapes, abound in nature.
Natural patterns of note

A Lichtenberg figure burned in wood by the application of a high voltage. Image by Chenoa van den Boogaard, used with permission
If you’ve ever seen a demonstration of a Lichtenberg figure, then you have a pretty good idea of how conservation of energy works in action. A Lichtenberg figure forms when high-voltage electricity is applied to an electrically insulating material, such as wood. From the moment the high-voltage electricity makes contact with the wood, it attempts to discharge along the path of least resistance. The result is a forked pattern, very similar to lightning. In fact, lightning is a naturally occurring, three-dimensional Lichtenberg figure.
Physarum polycephalum, otherwise known as slime mould, is a highly resilient single-celled organism capable of creating highly efficient networks between food sources. As slime mould spreads out in search of food, it forms a network of tendrils that connects each source it finds. Recently, researchers at the University of California, Santa Cruz decided to use the slime mould’s behaviour as a model for the tendrils of gas, dust and dark matter that connect galaxies in the universe. To their delight, they found the model was an excellent fit. Scientists at Queen’s University in Toronto also used slime mould to model existing Canadian highway systems with surprising accuracy. This research holds exciting possibilities for the use of slime mould models in the construction of future transportation networks.

Romanesco broccoli is a stunning example of a naturally forming fractal.
Image source: Wikipedia, CC BY-SA 4.0
Fractals are never-ending mathematical shapes that repeat at increasingly smaller scales. They can be seen in frost crystals, some types of mould, migrating cells, and in some plants such as the Romanesco broccoli. They present yet another fascinating example of the mathematical nature of our world.
Wherever you look, nature is always arranging itself in a way that will allow it the greatest gain using the least amount of energy. The repeating patterns that arise from this behaviour bring a semblance of order to chaos, allowing us to see the beauty of the mathematical relationships that underpin the natural world.
~30~
What other examples of fractals, fibonacci spirals, and Lichtenberg figures have you come across in nature? Drop us a line in Comments to let us know!





Time travel into the past is possible and into the future the traveler in time in order to arrive in the past must first go into the future and then must i call it the boomer effect must go back farther to arrive at the time in which one desires to arrive at reason is to try go in the past from relative would be impossible due to the pull of your present time frame to much electromagnetic constanance from present energy flux in your here and now one must first travel into the future farther depending on how far one wants to go back all past present and future remain fixed for it is governd by physics bound to a 4th dimensional reality given so it becomes possible to go back inthe future you dont have your electro magnetic field which holds your atoms together in a extreme gravitional density in this case going into pulls you out of its constant grip then you can achieve the necessary grid given you can produce a large of asuperconductor variable light and sound frequencys to permenate the electromagnetic field that holds you all together then you can invertably by pass the gravational pull that sets you in your now
Nice article Chenoa!
Short but well-written and full of good info, and nice pics.
One thing I didn’t know was the mold-galaxy parallelism. It always amazes me that there can be common patterns across such different size magnitudes. Our universe is awesome.
Keep up the good stuff! 🙂